MuJoCo Basics¶
mink is built on MuJoCo. This page covers the MuJoCo concepts relevant to inverse kinematics and explains how mink builds on them.
Model and Data¶
MuJoCo separates the model description from the state:
MjModel contains quantities that do not change over time—the robot’s kinematic tree, joint definitions, geometry, and physical properties. You create it once from an XML file.
MjData contains the state and quantities derived from it. The state
consists of time (data.time), generalized positions (data.qpos), and
generalized velocities (data.qvel).
import mujoco
model = mujoco.MjModel.from_xml_path("robot.xml")
data = mujoco.MjData(model)
Calling mujoco.mj_forward(model, data) runs the full forward pass and
updates derived quantities in data. mink’s update()
calls only what IK needs: mj_kinematics and mj_comPos. See MuJoCo’s
simulation pipeline
for details.
For a comprehensive introduction, see the official tutorial and documentation.
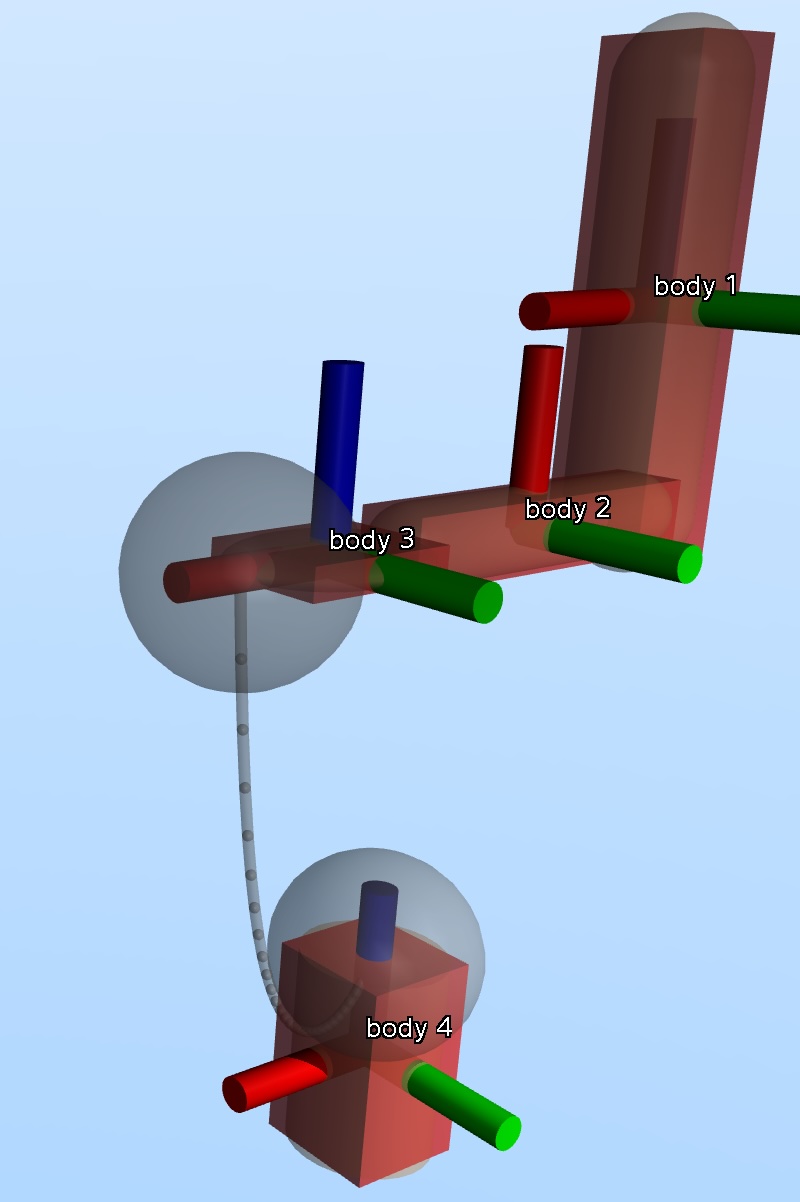
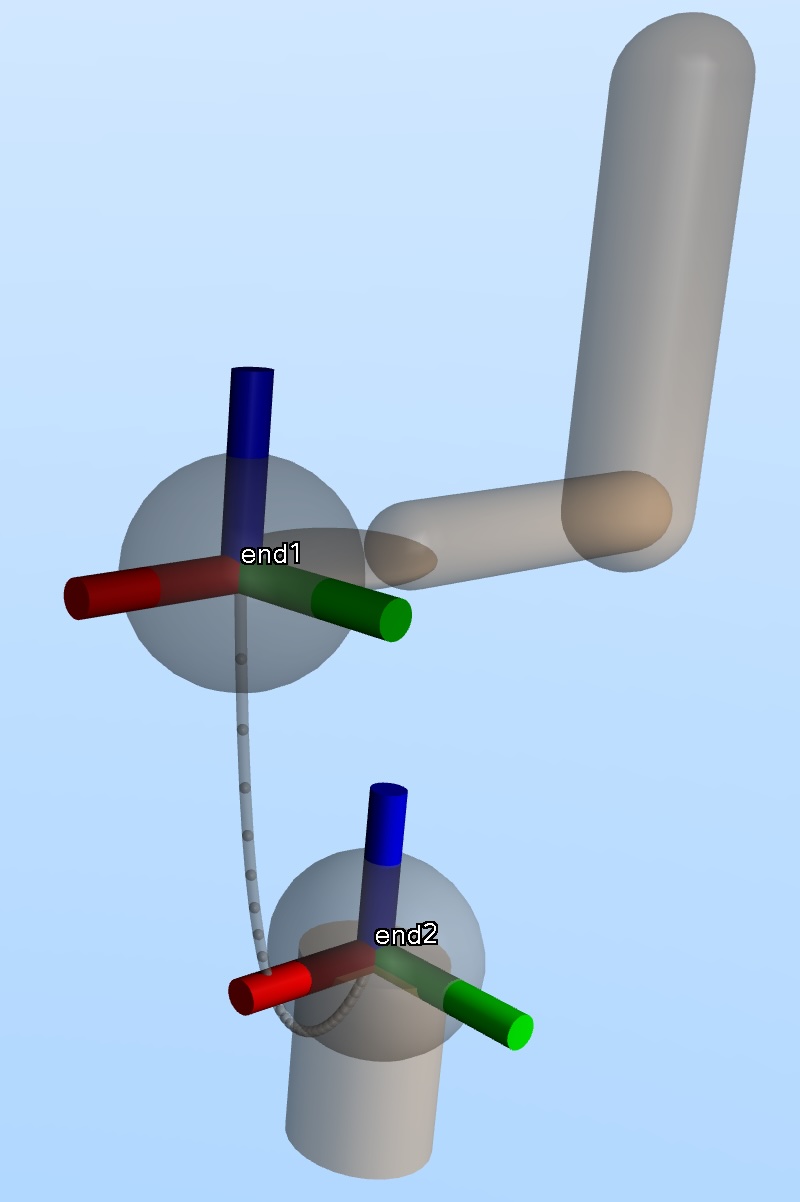
Frames¶
A frame is a coordinate system attached to an element in the model. MuJoCo has many frame types; mink focuses on three for inverse kinematics:
Note
In this example, the geom and inertial body frames coincide.
- Bodies (left)
The kinematic links of your robot. Each body has two frames: a frame used to define it and position child elements, and an inertial frame centered at the body’s center of mass and aligned with its principal axes of inertia. mink uses the inertial frame (
mjOBJ_BODY).- Geoms
Collision and visual geometry attached to bodies. Each geom has its own frame, which may be offset from the parent body.
- Sites (right)
Massless frames attached to bodies. Sites define points of interest— end-effectors, sensor locations, grasp points—without adding collision geometry. For IK, you typically define tasks on sites.
<body name="tool">
<site name="end_effector" pos="0 0 0.1"/>
</body>
Joints and Generalized Coordinates¶
Joints connect bodies and define how they can move:
hinge: Rotation about one axis (1 DOF)
slide: Translation along one axis (1 DOF)
ball: Spherical joint, quaternion representation (3 DOF, 4 values in qpos)
free: Unconstrained 6-DOF motion (6 DOF, 7 values in qpos)
MuJoCo uses scalar-first quaternions (wxyz), where w is the real component.
Joint positions are stored in data.qpos (generalized coordinates). For
robots with only hinge joints, qpos is the vector of joint angles.
Note
The dimension of qpos (model.nq) may differ from the number of
degrees of freedom (model.nv) when quaternion-based joints are present.
mink exposes both via configuration.nq and configuration.nv.
Coordinate System¶
MuJoCo uses a right-handed coordinate system. By default:
Z is up (gravity points in -Z)
X is forward
Y is left
Velocity and Jacobian Conventions¶
This section covers the frame conventions for velocities and Jacobians. If you just want to use mink, you can skip this—mink handles the conversions internally. This is useful if you need to interface with other libraries or understand what’s happening under the hood.
MuJoCo’s velocity convention¶
MuJoCo uses a mixed-frame representation for 6D velocities:
Linear velocity: world frame
Angular velocity: body frame
This follows from quaternion integration—angular velocities live in the quaternion’s tangent space, which is a local (body) frame.
MuJoCo’s Jacobian convention¶
MuJoCo’s mj_jacBody, mj_jacSite, and mj_jacGeom return Jacobians in
the local-world-aligned frame: the origin is at the frame, but axes are
aligned with the world. In Pinocchio terminology, this is LOCAL_WORLD_ALIGNED.
# MuJoCo returns a local-world-aligned Jacobian
jac = np.zeros((6, model.nv))
mujoco.mj_jacSite(model, data, jac[:3], jac[3:], site_id)
mink’s convention¶
mink uses body velocities (twists expressed in the local frame) and body Jacobians throughout. This is a consistent choice: the Jacobian and the velocity/error it maps to are in the same frame.
get_frame_jacobian() applies an adjoint transformation
to convert MuJoCo’s local-world-aligned Jacobian into a body Jacobian (LOCAL
in Pinocchio terminology):
# mink returns a body Jacobian
jac = configuration.get_frame_jacobian("end_effector", "site")
Similarly, task errors are computed as body twists via the right-minus operation
on SE(3). This ensures the relationship error = J @ dq is consistent, with
both sides in the body frame.
Note
mink uses right Jacobians (body perturbations), consistent with body velocities. For background on left vs right Jacobians on Lie groups, see A micro Lie theory.
Summary: what mink provides¶
mink’s Configuration wraps MuJoCo’s model and data, providing:
Poses in the world frame via
get_transform_frame_to_world()Body Jacobians in the local frame via
get_frame_jacobian()Inertia matrix via
get_inertia_matrix()
Internally, mink works entirely with body-frame quantities (velocities, errors, Jacobians), converting from MuJoCo’s conventions as needed.