In this blog post, we’re going to take a close look at Dex-Net 2.0: Deep Learning to Plan Robust Grasps with Synthetic Point Clouds and Analytic Grasp Metrics by Jeffrey Mahler, Jacky Liang, Sherdil Niyaz, Michael Laskey, Richard Doan, Xinyu Liu, Juan Aparicio Ojea, and Ken Goldberg.

Overview

TL, DR. This paper tackles grasp planning which is the task of finding a gripper configuration (pose and width) that maximizes a success metric subject to kinematic and collision constraints. The suggested approach is to train a Grasp Quality Convolutional Neural Network (GQ-CNN) on a large synthetic dataset of depth images with associated positive and negative grasps. Then during test time, one can sample various grasps from a depth image, feed each through the GQ-CNN, pick the one with the highest probability of success, and execute the grasp open-loop.

Variables

Let’s start by introducing the variables that appear in the paper.

• $x = (O, T_o, T_c, \gamma)$: the state describing the variable properties of the camera and objects in the environment, where:
  • $O$: the geometry and mass properties of the object.
  • $T_o, T_c$: 3D poses of the object and camera respectively.
  • $\gamma$: the coefficient of friction between the object and the gripper.
• $u = (p, \phi)$: a parallel-jaw grasp in 3D space, specified by a center $p = (x, y, z)$ relative to the camera and an angle in the table plane $\phi$.
• $y = R^{H \times W}$: a pointcloud represented as a depth image with height H and width W taken by the camera with known intrinsics $K$ and pose $T_c$.
• $S(u, x) \in \{0, 1\}$: a binary-valued grasp success metric, such as force closure.

Using these random variables, we can define a joint distribution $p(S, x, u, y)$ that models the inherent uncertainty associated with our assumptions, such as erroneous sensors readings (calibration error, noise, limiting pinhole model, etc.), and imprecise control (kinematic inaccuracies, etc.).

Goal. Ingest a depth image $u$ of an object in a scene with an associated grasp candidate $u$, and spit out the probability that $u$ will succeed under the above uncertainties. This is equivalent to predicting the robustness $Q$ of a grasp, defined as the expected value of $S$ conditioned on $u$ and $y$, i.e. $Q(u, y) = \mathbb{E}[S \vert u, y]$.

Solution. Use a neural network with weights $\theta$ to approximate the complex, high-dimensional function $Q$. Concretely,

$$\hat{\theta} = \arg \min_{\theta} \ \mathbb{E}_{p(S, u, x, y)} \big[L(S, Q_{\theta}(u, y)) \big]$$

And finally, using Monte-Carlo sampling of input-output pairs from our joint distribution, we obtain:

$$\hat{\theta} = \arg\min_{\theta} \sum_{i=1}^{N} L(S_i, Q_{\theta}(u_i, y_i))$$

where $(S_i, u_i, x_i, y_i) \sim p(S, x, u, y)$.

Generative Graphical Model

We can think of our joint $p(S, x, u, y)$ as a generative model of images, grasps and success metrics. The relationship between the different variables is illustrated in the graphical model below.

Graphical Model

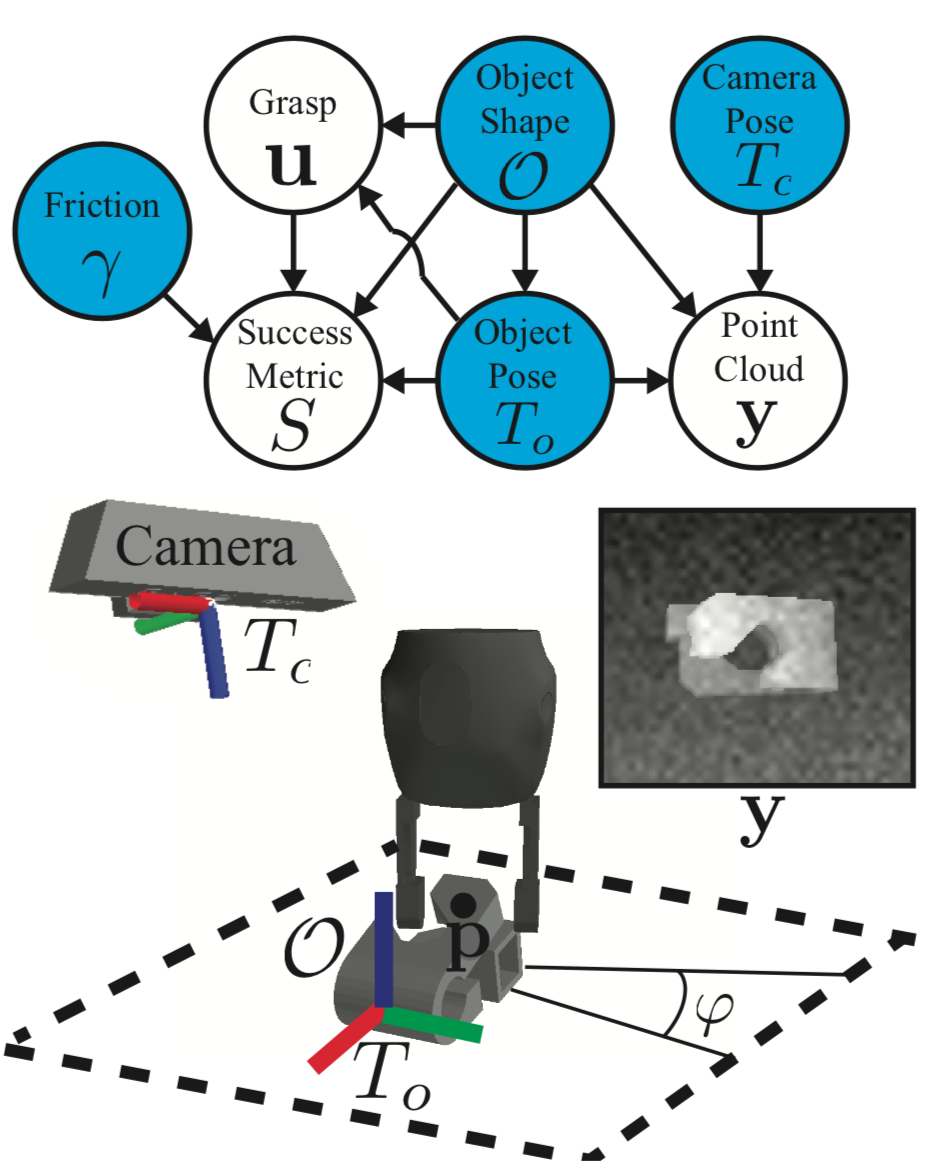
Using the chain rule, we can express the joint $p(S, x, u, y)$ as the product of 4 terms: $p(S \vert u, y, x)$, $p(u \vert x, y)$, $p(y \vert x)$ and $p(x)$. And since $S$ and $u$ are independent of $y$ (no arrow going from $y$ to $S$ or $u$), we can reduce the expression to

$$p(S, u, y, x) = {\color{red}{p(S \vert u, x)}} \cdot {\color{orange}{p(u \vert x)}} \cdot {\color{blue}{p(y \vert x)}} \cdot {\color{green}{p(x)}}$$

where:

• ${\color{green}{p(x)}}$ is the state distribution.
• ${\color{blue}{p(y \vert x)}}$ is the observation model, conditioned on the current state.
• ${\color{orange}{p(u \vert x)}}$ is the grasp candidate model, conditioned on the current state.
• ${\color{red}{p(S \vert u, x)}}$ is the analytic model of grasp success conditioned on the grasp candidate and current state.

The state $x = (O, T_o, T_c, \gamma)$ is represented by the blue nodes in the graphical model. Using the chain rule and independence properties, we can express its underlying distribution as the product of:

$$\begin{align*} {\color{green}{p(x)}} &= p(\gamma \vert T_c, T_o, O) \cdot p(T_c \vert T_o, O) \cdot p(T_o \vert O) \cdot p(O) \\ &= p(\gamma) \cdot p(T_c) \cdot p(T_o \vert O) \cdot p(O) \end{align*}$$

with:

• $p(\gamma)$: truncated Gaussian over friction coefficients.
• $p(O)$: discrete uniform distribution over 3D object models.
• $p(T_o \vert O)$: continuous uniform distribution over discrete set of stable object poses.
• $p(T_c)$: continuous uniform distribution over spherical coordinates and polar angle.

The grasp candidate model ${\color{orange}{p(u \vert x)}}$ is a uniform distribution over pairs of antipodal contact points on the object surface whose grasp axis is parallel to the table plane (we want top-down grasps), the observation model ${\color{blue}{p(y \vert x)}}$ is a rendered depth image of the scene corrupted with multiplicative and Gaussian Process noise, and the success model ${\color{red}{p(S \vert u, x)}}$ is a binary-valued reward function subject to 2 constraints: epsilon quality and collision freedom.

Now that we’ve examined the inner workings of our generative model $p$, let’s see how we can use it to generate the massive Dex-Net dataset.

Generating Dex-Net

To train our GQ-CNN, we need to generate i.i.d samples, consisting of depth images, grasps, and grasp robustness labels, by sampling from the generative joint $p(S, x, u, y)$.

Data Generation Pipeline

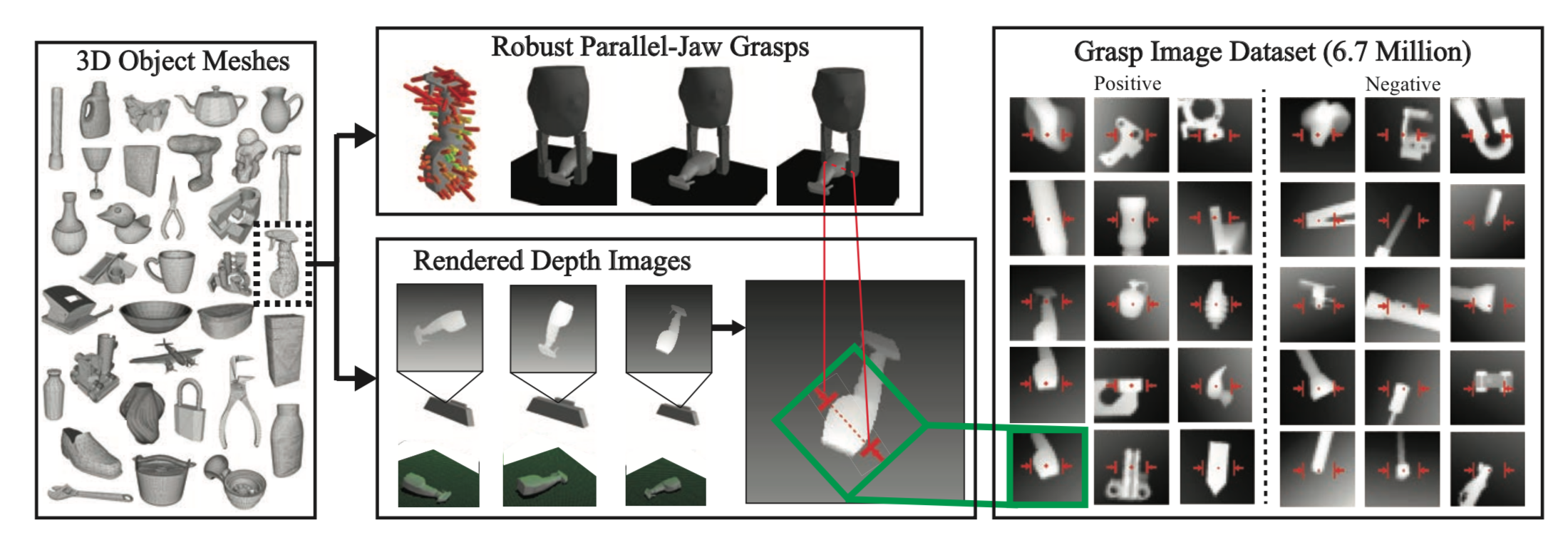
1. Randomly select, from a database of 1,500 meshes, a 3D object mesh using a discrete uniform distribution.
2. Randomly select, from a set of stable poses, a pose for this object using a continuous uniform distribution.
3. Use rejection sampling to generate top-down parallel-jaw grasps covering the surface of the object.
4. Randomly sample the camera pose (also from a continuous uniform distribution) and use it to render the object and its pose w.r.t to the camera into a depth image using ray tracing.
5. Classify the robustness of each sampled grasps to obtain a set of positive and negative grasps. Robustness is estimated using force closure probability which is a function of object pose, gripper pose, and friction coefficient uncertainty.

Training the GQ-CNN

Once the synthetic dataset has been generated, it becomes trivial to train the network.

Overview of the Model

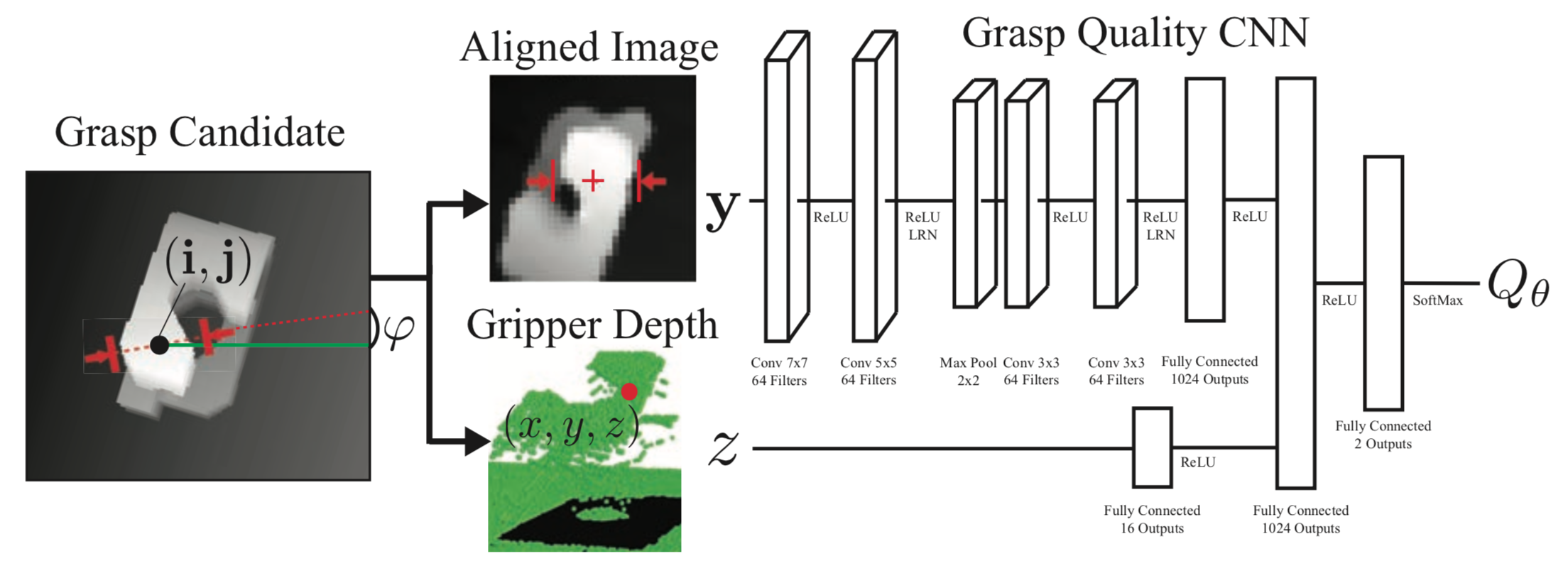
Remember how we mentioned that GQ-CNN takes as input a depth image and a grasp candidate? Well it actually turns out that the authors have a very clever way of encoding the grasp information into the depth image: they take a depth image and grasp candidate and transform the depth image such that the grasp pixel location $(i, j)$ – projected from the grasp position $(x, y)$ – is aligned with the image center and the grasp axis $\varphi$ corresponds to the middle row of the image. Then, at every iteration of SGD, we sample the transformed depth image and the remaining grasp variable $z$ (i.e the gripper depth from the camera), normalize the depth image to zero mean and unit standard deviation, and feed the tuple to the 18M parameter GQ-CNN model.

Note 1. The model is a typical deep learning architecture composed of convolutional, max-pool and fully-connected primitives.

Note 2. The depth alignment makes it easier for the model to train since it doesn’t have to worry about any rotational invariances. As for feeding the gripper depth to the model, I would think this is useful for pruning grasps that have the correct 2D position and orientation, but are too far away from the object (i.e. either not touching or barely touching).

Grasp Planning (Inference Time)

Once the model is trained, we can pair the QG-CNN with a policy of choice. The one used in the paper is $\pi_{\theta}(y) = \arg \max_{u \in C} Q_{\theta}(u, y)$ which amounts to sampling a set of predefined grasps from a depth image subject to a set of constraints $C$ (e.g. kinematic and collision constraints), scoring each grasp using the GQ-CNN, and finally executing the most robust grasp. There are two sampling strategies used to generate grasp candidates: antipodal grasp sampling and cross-entropy sampling.

Antipodal Grasp Sampling.

First, we perform edge detection by locating pixel areas with high gradient magnitude. This is especially useful since graspable regions usually correspond to contact points on opposite edges of an object.

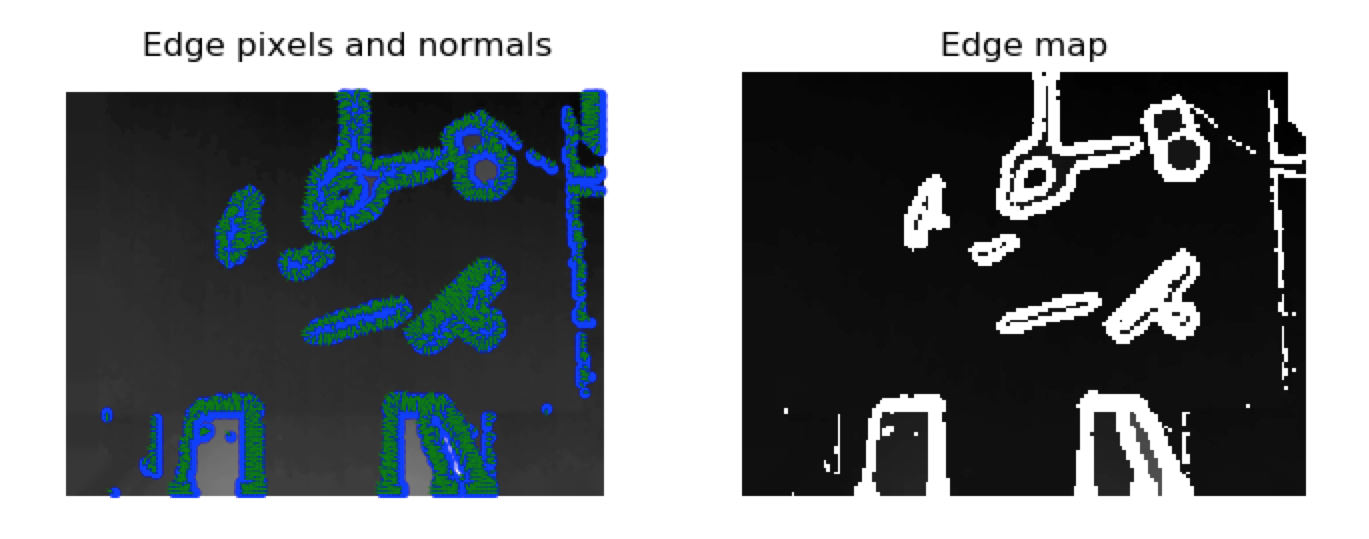
Then we sample pairs of pixels belonging to these areas to generate antipodal contact points on the object. We enforce the constraints that point pairs are parallel to the table plane.

We repeat this step until we reach the desired number of grasps, potentially increasing the friction coefficient if the amount is insufficient. In the final step, 2D grasps are deprojected to 3D grasps using the camera intrinsics and extrinsics and multiple grasps are obtained from the same contact points by discretizing the height starting from the object surface to the table surface ($h = 0$).

Cross Entropy Method.

Evolution of grasp robustness as the gripper center sweeps the depth image from top to bottom.

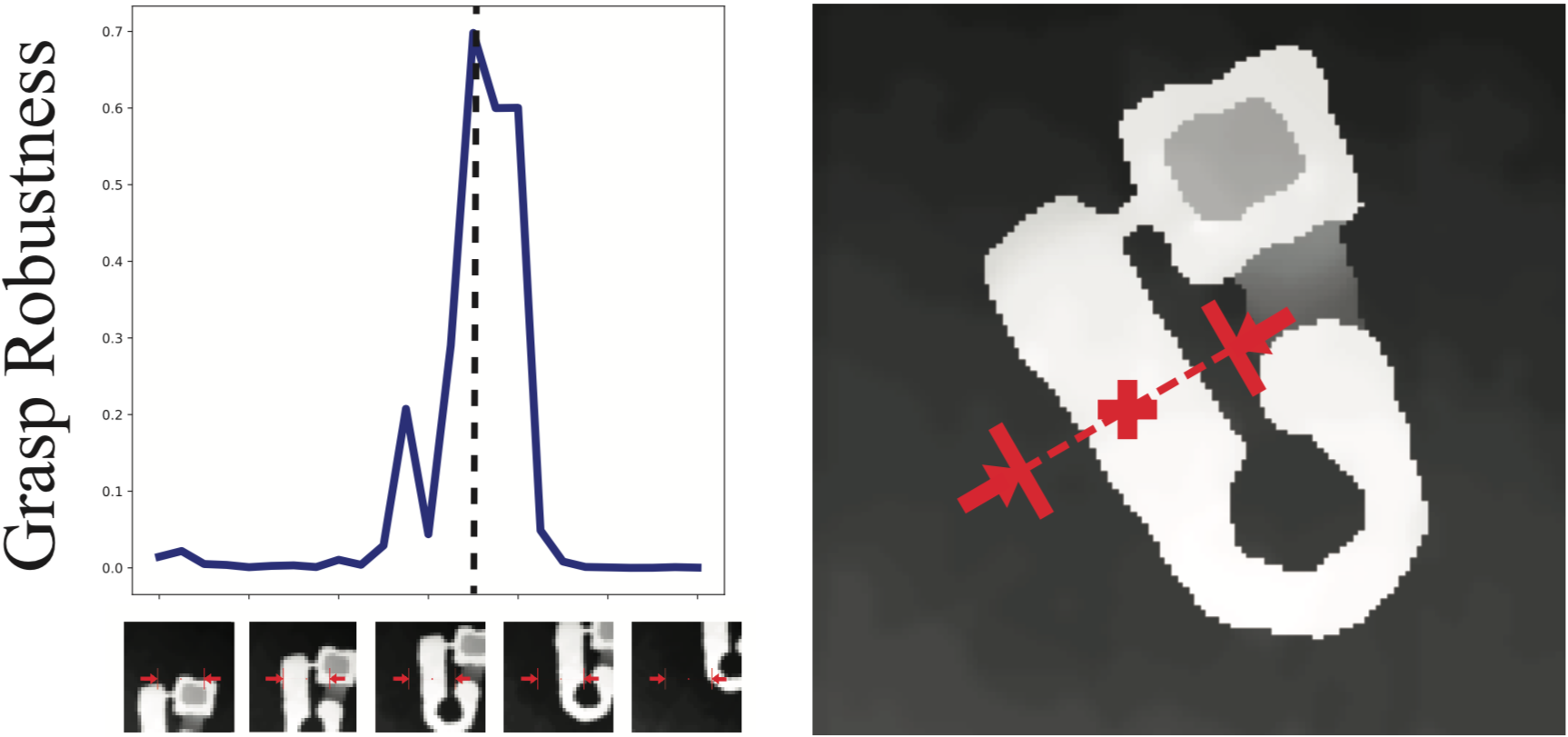
Randomly choosing a grasp from a set of candidates doesn’t work very well in cases where the grasping regions are small and require very precise gripper configurations. Taking a look at the image above, we can see that as we sweep candidate grasps from top to bottom, grasp robustness stays near zero and spikes momentarily when we reach the good, yet narrow grasping area. Thus, uniform sampling of grasp candidates is inefficient especially since we’re trying to perform real-time grasp planning.

This is where importance sampling – one of my favorite techniques – can help! We can modify our sampling strategy such that at every iteration, we refit the candidate distribution to the grasps with the highest predicted robustness. The algorithm to perform this fitting is the cross-entropy method (CEM) which tries to minimize the cross-entropy between a mixture of gaussians and the top-k percentile of grasps ranked by GQ-CNN. The result is that at every iteration, we are more likely to sample grasps with high-robustness values (grasps in the spike area) and converge to an optimal grasp candidate. This fitting process is illustrated below.

Discussion

• The sampling of grasps is inefficient. It would be interesting to extend the GQ-CNN to a fully-convolutional architecture where robustness labels can be computed for every pixel in the depth image in a single forward pass.
• Dex-Net is open-loop which means that once a grasp candidate has been picked, it is executed blindly with no visual feedback. This sets it up for failure when camera calibration is imprecise or the environment it is placed in is dynamic and susceptible to change.
• If we can speed-up Dex-Net by creating a smaller, fully-convolutional GQ-CNN, we may be able to run it at a high enough frequency to incorporate visual feedback and close the loop.